Description
Use the remainder theorem to find the remainder when f(x) is divided by x-(1/3). Then use the factor theorem to determine whether x-(1/3) is a factor of f(x).
f(x)= 3x^4-x^3+15x-5
Then is x-(1/3) a factor of f(x)?
Really appreciate your help!! Thank you!

Explanation & Answer

Thank you for the opportunity to help you with your question!
-------------------------------------------------------------------------------
The remainder theorem states that the remainder of the division of a polynomial  by a linear polynomial
by a linear polynomial 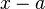 is equal to
is equal to 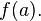
To find the remainder when f(x) is divided by x-(1/3) using remainder theorem,
substitute x = 1/3 in f(x).
So the remainder is 0.
The factor theorem states that a polynomial  has a factor
has a factor  if and only if
if and only if  .
.
We showed that .
Hence, by factor theorem is a factor of f(x).
-------------------------------------------------------------------------------
Please let me know if you need any clarification. I'm always happy to answer your questions.
Review
Review






24/7 Homework Help
Stuck on a homework question? Our verified tutors can answer all questions, from basic math to advanced rocket science!






Similar Content
Related Tags










